电解水过程中,在阴极发生的析氢反应(Hydrogen Evolution Reaction,HER)和在阳极发生的析氧反应(Oxygen Evolution Reaction,OER)的Tafel斜率受到反应机理和决速步骤的影响,本文对 HER 和 OER 反应机理进行系统性总结。
1 HER 反应机理
HER过程一般经过两步反应步骤:
第一步:质子被还原并吸附到催化剂表面(S)的过程,称为 Volmer 反应:
H A + S + e − = S – H ∗ + A − \mathrm{HA\ + \ S\ +\ e^- = S\text{\textendash}H^*\ +\ A^-}
HA + S + e − = S – H ∗ + A −
第二步:第二个质子的电化学还原和H2分子生成过程(Heyrovsky反应),此步为电化学伴随化学过程,也称电化学脱附步骤:
S – H ∗ + H A + e − = S + H 2 + A − \mathrm{S\text{\textendash}H^*\ +\ HA\ + \ e^- = S\ +\ H_2\ +\ A^-}
S – H ∗ + HA + e − = S + H 2 + A −
或两个吸附氢原子结合生成氢气的反应过程(Tafel反应),也称复合脱附步骤:
2 S – H ∗ = 2 S + H 2 \mathrm{2S\text{\textendash}H* = 2S\ +\ H_2}
2S – H ∗ = 2S + H 2
式中, A − \mathrm{A^-} A − A − = H 2 O \mathrm{A^-=H_2O} A − = H 2 O A − = O H − \mathrm{A^-=OH^-} A − = O H −
按照第二步反应的不同,HER 反应机理可分为 Tafel-Volmer 机理和 Heyrovsky-Volmer 机理。在上一节我们知道 Tafel 斜率与反应过程,尤其是决速步有关,那么下面我们就推导碱性条件下各反应步骤为决速步时 Tafel 斜率的变化。
H 2 O + S + e − = S – H ∗ + O H − ( V ) S – H ∗ + H 2 O + e − = S + H 2 + O H − ( H ) 2 S – H ∗ = 2 S + H 2 ( T ) \begin{aligned}
\mathrm{H_2O + S +e^-} &=\mathrm{S\text{\textendash}H^* +OH^-}&(V)\\
\mathrm{S\text{\textendash}H^* + H_2O + e^- }&=\mathrm{S + H_2 +OH^-}&(H)\\
\mathrm{2S\text{\textendash}H^* }& = \mathrm{2S + H_2}&(T)
\end{aligned} H 2 O + S + e − S – H ∗ + H 2 O + e − 2S – H ∗ = S – H ∗ + O H − = S + H 2 + O H − = 2S + H 2 ( V ) ( H ) ( T )
根据反应式,按照 Langmuir 模型写出各反应的速率方程,其中 θ 1 \theta_1 θ 1 ν ± i \nu_{\pm i} ν ± i k ± i k_{\pm i} k ± i m o l ⋅ c m − 2 ⋅ s − 1 mol\cdot cm^{-2}\cdot s^{-1} m o l ⋅ c m − 2 ⋅ s − 1 α 1 \alpha_1 α 1 α 2 \alpha_2 α 2 前文 论述,电势降低有利于电极表面电子的逸出,进而降低还原反应活化能。因此,所有还原反应指数项应随 E 的减小而增大)。
V V = ν + 1 − ν − 1 = k + 1 ( 1 − θ 1 ) e ( α 1 − 1 ) F E R T − k − 1 θ 1 e α 1 F E R T V H = ν + 2 − ν − 2 = k + 2 θ 1 e ( α 2 − 1 ) F E R T − k − 2 ( 1 − θ 1 ) e α 2 F E R T V T = ν + 3 − ν − 3 = k + 3 2 θ 1 2 − k − 3 2 ( 1 − θ 1 ) 2 \begin{aligned}
V_V&=\nu_{+1}-\nu_{-1}=k_{+1}(1-\theta_1)e^{\frac{(\alpha_1-1)FE}{RT}}-k_{-1}\theta_1e^{\frac{\alpha_1FE}{RT}}
\\
V_H&=\nu_{+2}-\nu_{-2}=k_{+2}\theta_1e^{\frac{(\alpha_2-1)FE}{RT}}-k_{-2}(1-\theta_1)e^{\frac{\alpha_2FE}{RT}}
\\
V_T&=\nu_{+3}-\nu_{-3}=k_{+3}{}^2\theta_1{}^2-k_{-3}{}^2(1-\theta_1){}^2
\end{aligned} V V V H V T = ν + 1 − ν − 1 = k + 1 ( 1 − θ 1 ) e RT ( α 1 − 1 ) FE − k − 1 θ 1 e RT α 1 FE = ν + 2 − ν − 2 = k + 2 θ 1 e RT ( α 2 − 1 ) FE − k − 2 ( 1 − θ 1 ) e RT α 2 FE = ν + 3 − ν − 3 = k + 3 2 θ 1 2 − k − 3 2 ( 1 − θ 1 ) 2
当 T-V 机理中 Volmer 步骤为速控步时,可认为 Tafel 步骤的净速率等于 0,而整个反应的速率近似为 Volmer 步骤中正反应的速率 v + 1 v_{+1} v + 1 v + 3 = v − 3 v_{+3}=v_{-3} v + 3 = v − 3 V V ≈ v + 1 V_V\approx v_{+1} V V ≈ v + 1
令 α 1 = α 2 = 0.5 \alpha_1=\alpha_2=0.5 α 1 = α 2 = 0.5 v + 3 = v − 3 v_{+3}=v_{-3} v + 3 = v − 3
θ 1 1 − θ 1 = k − 3 k + 3 ( V . 1 ) θ 1 = k − 3 k − 3 + k + 3 ( V . 2 ) \begin{aligned}
\frac{\theta_1}{1-\theta_1}&=\sqrt\frac{k_{-3}}{k_{+3}}&(V.1)\\
\theta_1&=\frac{\sqrt{k_{-3}}}{\sqrt{k_{-3}}+\sqrt{k_{+3}}}&(V.2)
\end{aligned} 1 − θ 1 θ 1 θ 1 = k + 3 k − 3 = k − 3 + k + 3 k − 3 ( V .1 ) ( V .2 )
进而得到
V ≈ v + 1 = k + 1 ( 1 − θ 1 ) e − F E 2 R T = k + 1 k + 3 k − 3 + k + 3 exp ( − F E 2 R T ) ( V . 3 ) \begin{aligned}
V\approx v_{+1}&=k_{+1}(1-\theta_1)e^{-\frac{FE}{2RT}}
\\
&=\frac{k_{+1}\sqrt{k_{+3}}}{\sqrt{k_{-3}}+\sqrt{k_{+3}}}\exp\left(-\frac{FE}{2RT}\right)&(V.3)
\end{aligned} V ≈ v + 1 = k + 1 ( 1 − θ 1 ) e − 2 RT FE = k − 3 + k + 3 k + 1 k + 3 exp ( − 2 RT FE ) ( V .3 )
反应速率的单位是 m o l ⋅ c m − 2 ⋅ s − 1 mol\cdot cm^{-2}\cdot s^{-1} m o l ⋅ c m − 2 ⋅ s − 1
i F = 2 F V = 2 F k ′ exp ( − F E 2 R T ) i_F=2FV=2Fk'\exp\left(-\frac{FE}{2RT}\right)
i F = 2 F V = 2 F k ′ exp ( − 2 RT FE )
求 Tafel 斜率,即求 ∂ E ∂ lg i \frac{\partial E}{\partial \lg i } ∂ l g i ∂ E
∂ E ∂ lg i = − 2 × 2.3 R T F = − 118 m V ⋅ d e c − 1 \frac{\partial E}{\partial \lg i }=- \frac{2\times 2.3 RT}{F}=-118 mV\cdot dec^{-1}
∂ lg i ∂ E = − F 2 × 2.3 RT = − 118 mV ⋅ d e c − 1
这代表着,过电势的值每降低 118 mV,电流密度提升 10 倍(在阴极还原反应中过电势的值是负值)。
当 H-V 机理中 Heyrovsky 步骤步骤为决速步时,可认为 v + 1 = v − 1 v_{+1}=v_{-1} v + 1 = v − 1 V H ≈ v + 2 V_H\approx v_{+2} V H ≈ v + 2
令 α 1 = α 2 = 0.5 \alpha_1=\alpha_2=0.5 α 1 = α 2 = 0.5 v + 1 = v − 1 v_{+1}=v_{-1} v + 1 = v − 1
k + 1 ( 1 − θ 1 ) e − F E 2 R T = k − 1 θ 1 e F E 2 R T ( H . 1 ) θ 1 = k + 1 k + 1 + k − 1 e F E R T ( H . 2 ) \begin{aligned}
k_{+1}(1-\theta_1)e^{-\frac{FE}{2RT}}&=k_{-1}\theta_1e^{\frac{FE}{2RT}}&(H.1)
\\
\theta_1&=\frac{k_{+1}}{k_{+1}+k_{-1}e^{\frac{FE}{RT}}}&(H.2)
\end{aligned} k + 1 ( 1 − θ 1 ) e − 2 RT FE θ 1 = k − 1 θ 1 e 2 RT FE = k + 1 + k − 1 e RT FE k + 1 ( H .1 ) ( H .2 )
进而有
V ≈ v + 2 = k + 2 k + 1 e − F E 2 R T k + 1 + k − 1 e F E R T ( H . 3 ) \begin{aligned}
V\approx v_{+2}&=\frac{k_{+2}k_{+1}e^{-\frac{FE}{2RT}}}{k_{+1}+k_{-1}e^{\frac{FE}{RT}}}&(H.3)
\end{aligned} V ≈ v + 2 = k + 1 + k − 1 e RT FE k + 2 k + 1 e − 2 RT FE ( H .3 )
当 E 很小(过电势的绝对值很大)时,分母中的 k + 1 k_{+1} k + 1
V = k + 2 k + 1 e − F E 2 R T k − 1 e F E R T = k ′ exp ( − 3 F E 2 R T ) ( H . 4 ) \begin{aligned}
V&=\frac{k_{+2}k_{+1}e^{-\frac{FE}{2RT}}}{k_{-1}e^{\frac{FE}{RT}}}\\
&=k'\exp\left(- \frac{3FE}{2RT}\right)
&(H.4)\\
\end{aligned} V = k − 1 e RT FE k + 2 k + 1 e − 2 RT FE = k ′ exp ( − 2 RT 3 FE ) ( H .4 )
求 Tafel 斜率:
∂ E ∂ lg i = − 2 × 2.3 R T 3 F = − 39 m V ⋅ d e c − 1 \frac{\partial E}{\partial \lg i }=- \frac{2\times 2.3 RT}{3F}=-39 mV\cdot dec^{-1}
∂ lg i ∂ E = − 3 F 2 × 2.3 RT = − 39 mV ⋅ d e c − 1
当 T-V 机理中 Tafel 步骤为决速步时,可认为v + 1 = v − 1 v_{+1}=v_{-1} v + 1 = v − 1 V T ≈ v + 3 V_T\approx v_{+3} V T ≈ v + 3
由上述的 H-V 机理得到
θ 1 = k + 1 k + 1 + k − 1 e F E R T \theta_1=\frac{k_{+1}}{k_{+1}+k_{-1}e^{\frac{FE}{RT}}}
θ 1 = k + 1 + k − 1 e RT FE k + 1
令 α 1 = α 2 = 0.5 \alpha_1=\alpha_2=0.5 α 1 = α 2 = 0.5
V T ≈ v + 3 = k + 3 θ 1 2 = k + 3 k + 1 2 ( k + 1 + k − 1 e F E R T ) 2 ( T . 1 ) \begin{aligned}
V_T\approx v_{+3}&=k_{+3}\theta_1{}^2\\
&=
\frac{k_{+3}k_{+1}{}^2}{(k_{+1}+k_{-1}e^{\frac{FE}{RT}})^2}&(T.1)
\end{aligned} V T ≈ v + 3 = k + 3 θ 1 2 = ( k + 1 + k − 1 e RT FE ) 2 k + 3 k + 1 2 ( T .1 )
当 E 较大(过电势的绝对值较小)时分母中的 k + 1 k_{+1} k + 1
V = k + 3 k + 1 2 k − 1 2 e 2 F E R T = k ′ exp ( − 2 F E R T ) ( T . 2 ) \begin{aligned}
V&=
\frac{k_{+3}k_{+1}{}^2}{k_{-1}{}^2e^{\frac{2FE}{RT}}}
\\
&=k'\exp\left(-\frac{2FE}{RT}\right)
&(T.2)
\end{aligned} V = k − 1 2 e RT 2 FE k + 3 k + 1 2 = k ′ exp ( − RT 2 FE ) ( T .2 )
求 Tafel 斜率:
∂ E ∂ lg i = − 2.3 R T 2 F = − 30 m V ⋅ d e c − 1 \frac{\partial E}{\partial \lg i }=- \frac{2.3 RT}{2F}=-30 mV\cdot dec^{-1}
∂ lg i ∂ E = − 2 F 2.3 RT = − 30 mV ⋅ d e c − 1
以上的推导说明,Tafel 斜率会随反应机理和过电势的变化而变化。
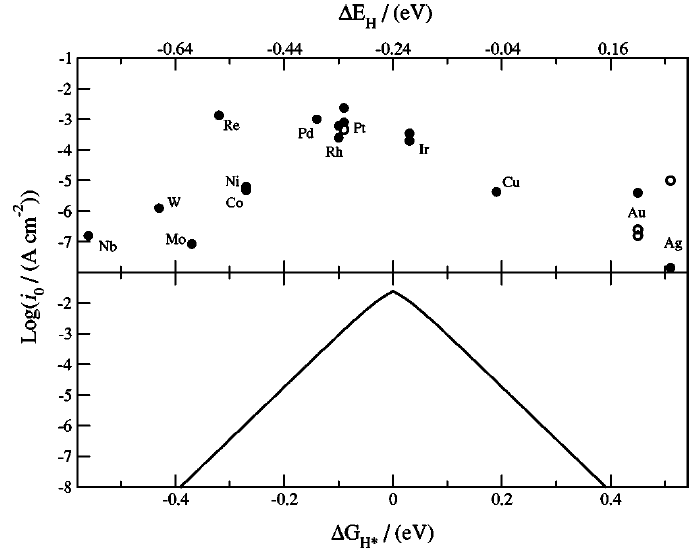
J.K.Norskov 等[1] 通过 DFT 理论计算得到氢在不同金属表面的吸附能,并测量各种金属的交换电流密度与吸附能的关系,得到下图所示的火山型曲线。这说明HER催化反应同样遵循 Sabatier 规则。
图 1 交换电流密度与吸附能的关系,图源[1] 由上面的火山图可知,Pt 族金属处于火山顶端附近,说明它们有最佳的 HER 催化性能。事实上,Pt 电极确实被广泛用作 PEM(质子交换膜)电解池的阴极材料,但是贵金属的稀缺性和高成本限制了其大规模应用。因此,研究者们主要通过如下两种技术路线降低 HER 催化剂的成本:
(1)降低贵金属的用量:通过将金属纳米粒子负载到高比表面积基底上,可以显著提高贵金属的利用率。
(2)开发廉价高效的非贵金属催化剂。某些非贵金属(尤其是过渡金属)的氧化物、氢氧化物、硫化物和磷化物具有适宜的氢吸附能,通过对其进行形貌调控和电子状态调控进一步优化其HER性能,可使其催化活性达到或超过贵金属催化剂,如MoS2 。
2 OER 反应机理
OER 过程是四电子转移过程,其反应步骤要比两电子转移的HER反应复杂得多。本节我们介绍常见的OER反应机理,并尝试推导它们的Tafel斜率。
研究者通过对 OER 反应长期的研究,提出了两大类催化机理,第一类是传统的吸附催化机理(Absorbate Evolution Mechanism,AEM),另一类是晶格氧催化机理(Lattice Oxygem Mechanism,LOM)。我们将对这两种机理进行简要介绍,并对某些机理进行动力学计算。
2.1 AEM 机理
AEM 机理基于吸附催化机理,特征在于催化剂本身所含的氧原子不参与反应(即催化剂表面的氧原子不会转移到产物中)。研究者们基于 OER 反应的 Tafel 斜率,提出了如下的反应历程 A1(又称复合脱附机理):
S + H 2 O = S – O H a d s + H + + e − ( A 1 S 1 ) S + O H a d s = S – O a d s + H + + e − ( A 1 S 2 ) 2 S – O a d s = 2 S + O 2 ( A 1 S 3 ) \begin{aligned}
\mathrm{S + H_2O }&= \mathrm{S\text{\textendash}OH_{ads} + H^+ +e^-} &(A1S1)\\
\mathrm{S + OH_{ads} }&= \mathrm{S\text{\textendash}O_{ads} + H^+ +e^-}&(A1S2)\\
\mathrm{2S\text{\textendash}O_{ads}}&= \mathrm{2S + O_2}&(A1S3)
\end{aligned} S + H 2 O S + O H ads 2S – O ads = S – O H ads + H + + e − = S – O ads + H + + e − = 2S + O 2 ( A 1 S 1 ) ( A 1 S 2 ) ( A 1 S 3 )
式中,S 表示金属氧化物的活性位点;S – O H a d s \mathrm{S\text{\textendash}OH_{ads}} S – O H ads S – O a d s \mathrm{S\text{\textendash}O_{ads}} S – O ads
另外,研究者们基于热力学理论计算,提出了另外一条反应历程 A2(此历程又称为亲核进攻机理):
S + H 2 O = S – O H + H + + e − ( A 2 S 1 ) S – O H = S – O + H + + e − ( A 2 S 2 ) S – O + H 2 O = S – O O H + H + + e − ( A 2 S 3 ) S – O O H = S + O 2 + H + + e − ( A 2 S 4 ) \begin{aligned}
\mathrm{S + H_2O }&= \mathrm{S\text{\textendash}OH + H^+ +e^-}&(A2S1)
\\
\mathrm{S\text{\textendash}OH }&= \mathrm{S\text{\textendash}O + H^+ + e^-}&(A2S2)
\\
\mathrm{S\text{\textendash}O + H_2O } &= \mathrm{S\text{\textendash}OOH + H^+ + e^-}&(A2S3)
\\
\mathrm{S\text{\textendash}OOH } &= \mathrm{S + O_2 + H^+ + e^-}&(A2S4)
\end{aligned} S + H 2 O S – OH S – O + H 2 O S – OOH = S – OH + H + + e − = S – O + H + + e − = S – OOH + H + + e − = S + O 2 + H + + e − ( A 2 S 1 ) ( A 2 S 2 ) ( A 2 S 3 ) ( A 2 S 4 )
该机理相比于复合脱附机理,特征在于所有步骤只涉及一个活性位点。我们稍后会探讨这两种机理哪种更接近于实际情况。现在,我们针对复合脱附机理进行 Tafel 斜率的推导。
2.1.1 复合脱附机理(A1)
首先列出各反应的反应速率方程:
V 1 = ν + 1 − ν − 1 = k + 1 ( 1 − θ 1 − θ 2 ) e α 1 F E R T − k − 1 θ 1 e ( α 1 − 1 ) F E R T ( 1 ) V 2 = ν + 2 − ν − 2 = k + 2 θ 1 e α 2 F E R T − k − 2 θ 2 e ( α 2 − 1 ) F E R T ( 2 ) V 3 = ν + 3 − ν − 3 = k + 3 θ 2 2 − k − 3 ( 1 − θ 1 − θ 2 ) 2 ( 3 ) \begin{aligned}
V_1&=\nu_{+1}-\nu_{-1}=k_{+1}(1-\theta_1-\theta_2)e^{\frac{\alpha_1FE}{RT}}-k_{-1}\theta_1e^{\frac{(\alpha_1-1)FE}{RT}}&(1)
\\
V_2&=\nu_{+2}-\nu_{-2}=k_{+2}\theta_1e^{\frac{\alpha_2FE}{RT}}-k_{-2}\theta_2e^{\frac{(\alpha_2-1)FE}{RT}}&(2)
\\
V_3&=\nu_{+3}-\nu_{-3}=k_{+3}\theta_2{}^2-k_{-3}(1-\theta_1-\theta_2)^2&(3)
\end{aligned} V 1 V 2 V 3 = ν + 1 − ν − 1 = k + 1 ( 1 − θ 1 − θ 2 ) e RT α 1 FE − k − 1 θ 1 e RT ( α 1 − 1 ) FE = ν + 2 − ν − 2 = k + 2 θ 1 e RT α 2 FE − k − 2 θ 2 e RT ( α 2 − 1 ) FE = ν + 3 − ν − 3 = k + 3 θ 2 2 − k − 3 ( 1 − θ 1 − θ 2 ) 2 ( 1 ) ( 2 ) ( 3 )
假设在电极反应过程中的 H + \mathrm{H^+} H + O 2 \mathrm{O_2} O 2 S 1 \mathrm{S1} S1 S 2 \mathrm{S2} S2 S 3 \mathrm{S3} S3 V 1 \mathrm{V_1} V 1 V 2 \mathrm{V_2} V 2 V 3 \mathrm{V_3} V 3
式中:
ν ± i \nu_{\pm i} ν ± i k ± i k_{\pm i} k ± i m o l ⋅ c m − 2 ⋅ s − 1 mol\cdot cm^{-2}\cdot s^{-1} m o l ⋅ c m − 2 ⋅ s − 1 α 1 \alpha_1 α 1 α 2 \alpha_2 α 2 S 1 \mathrm{S1} S1 S 2 \mathrm{S2} S2 θ 1 \theta_1 θ 1 θ 2 \theta_2 θ 2 S – O H a d s \mathrm{S\text{\textendash}OH_{ads}} S – O H ads S – O a d s \mathrm{S\text{\textendash}O_{ads}} S – O ads
下面推导各反应历程对应的 Tafel 斜率。
若 S 1 \mathrm{S1} S1
此时, V 1 ≈ ν + 1 , ν + 2 ≈ ν − 2 , ν + 3 ≈ ν − 3 V_1\approx \nu_{+1},\ \nu_{+2}\approx \nu_{-2}, \ \nu_{+3}\approx \nu_{-3} V 1 ≈ ν + 1 , ν + 2 ≈ ν − 2 , ν + 3 ≈ ν − 3 α 1 = α 2 = 0.5 \alpha_1=\alpha_2=0.5 α 1 = α 2 = 0.5
k + 2 θ 1 e F E 2 R T = k − 2 θ 2 e − F E 2 R T ( A 1 S 1.1 ) k + 3 θ 2 2 = k − 3 ( 1 − θ 1 − θ 2 ) 2 ( A 1 S 1.2 ) \begin{aligned}
k_{+2}\theta_1e^{\frac{FE}{2RT}}&=k_{-2}\theta_2e^{\frac{-FE}{2RT}}&(A1S1.1)
\\
k_{+3}\theta_2{}^2&=k_{-3}(1-\theta_1-\theta_2)^2&(A1S1.2)
\end{aligned} k + 2 θ 1 e 2 RT FE k + 3 θ 2 2 = k − 2 θ 2 e 2 RT − FE = k − 3 ( 1 − θ 1 − θ 2 ) 2 ( A 1 S 1.1 ) ( A 1 S 1.2 )
可得
V 1 = k + 1 ( 1 − θ 1 − θ 2 ) e F E 2 R T = k + 1 k + 2 k + 3 e F E 2 R T k + 2 k + 3 + k + 2 k − 3 + k − 2 k − 3 e − F E R T ( A 1 S 1.3 ) \begin{aligned}
V_1&=k_{+1}(1-\theta_1-\theta_2)e^{\frac{FE}{2RT}}\\
&=\frac{k_{+1}k_{+2}\sqrt{k_{+3}}e^{\frac{FE}{2RT}}}{k_{+2}\sqrt{k_{+3}}+k_{+2}\sqrt{k_{-3}}+k_{-2}\sqrt{k_{-3}}e^{-\frac{FE}{RT}}}
&(A1S1.3)
\end{aligned} V 1 = k + 1 ( 1 − θ 1 − θ 2 ) e 2 RT FE = k + 2 k + 3 + k + 2 k − 3 + k − 2 k − 3 e − RT FE k + 1 k + 2 k + 3 e 2 RT FE ( A 1 S 1.3 )
在低过电位区,式 S 1.3 S1.3 S 1.3 k + 2 k + 3 + k + 2 k − 3 k_{+2}\sqrt{k_{+3}}+k_{+2}\sqrt{k_{-3}} k + 2 k + 3 + k + 2 k − 3
V = k + 1 k + 2 k + 3 e F E 2 R T k − 2 k − 3 e − F E R T = k ′ exp ( 3 F E 2 R T ) ( A 1 S 1.4 ) i F = n F V = 4 F k ′ exp ( 3 F E 2 R T ) ( A 1 S 1.5 ) ∂ Δ E ∂ lg i = 2 × 2.3 R T 3 F = 39 m V ⋅ d e c − 1 \begin{aligned}
V
&=\frac{k_{+1}k_{+2}\sqrt{k_{+3}}e^{\frac{FE}{2RT}}}{k_{-2}\sqrt{k_{-3}}e^{-\frac{FE}{RT}}}\\
&=k'\exp\left(\frac{3FE}{2RT}\right)
&(A1S1.4)\\
\\
i_F&=nFV=4Fk'\exp\left(\frac{3FE}{2RT}\right)
&(A1S1.5)\\
\\
\frac{\partial\Delta E}{\partial \lg i }&= \frac{2\times 2.3 RT}{3F}=39 mV\cdot dec^{-1}
\end{aligned} V i F ∂ lg i ∂ Δ E = k − 2 k − 3 e − RT FE k + 1 k + 2 k + 3 e 2 RT FE = k ′ exp ( 2 RT 3 FE ) = n F V = 4 F k ′ exp ( 2 RT 3 FE ) = 3 F 2 × 2.3 RT = 39 mV ⋅ d e c − 1 ( A 1 S 1.4 ) ( A 1 S 1.5 )
在高过电位区,式 S 1.3 S1.3 S 1.3 k − 2 k − 3 e − F E R T k_{-2}\sqrt{k_{-3}}e^{-\frac{FE}{RT}} k − 2 k − 3 e − RT FE
V = k + 1 k + 2 k + 3 e F E 2 R T k + 2 k + 3 + k + 2 k − 3 = k ′ exp ( F E 2 R T ) ( A 1 S 1.6 ) i F = n F V = 4 F k ′ exp ( F E 2 R T ) ( A 1 S 1.7 ) ∂ Δ E ∂ lg i = 2 × 2.3 R T F = 118 m V ⋅ d e c − 1 \begin{aligned}
V
&=\frac{k_{+1}k_{+2}\sqrt{k_{+3}}e^{\frac{FE}{2RT}}}{k_{+2}\sqrt{k_{+3}}+k_{+2}\sqrt{k_{-3}}}\\
&=k'\exp\left(\frac{FE}{2RT}\right)
&(A1S1.6)\\
\\
i_F&=nFV=4Fk'\exp\left(\frac{FE}{2RT}\right)
&(A1S1.7)\\
\\
\frac{\partial\Delta E}{\partial \lg i }&= \frac{2\times 2.3 RT}{F}=118 mV\cdot dec^{-1}
\end{aligned} V i F ∂ lg i ∂ Δ E = k + 2 k + 3 + k + 2 k − 3 k + 1 k + 2 k + 3 e 2 RT FE = k ′ exp ( 2 RT FE ) = n F V = 4 F k ′ exp ( 2 RT FE ) = F 2 × 2.3 RT = 118 mV ⋅ d e c − 1 ( A 1 S 1.6 ) ( A 1 S 1.7 )
若 S 2 \mathrm{S2} S2
此时, V 2 ≈ ν + 2 , ν + 1 ≈ ν − 1 , ν + 3 ≈ ν − 3 V_2\approx \nu_{+2},\ \nu_{+1}\approx \nu_{-1}, \ \nu_{+3}\approx \nu_{-3} V 2 ≈ ν + 2 , ν + 1 ≈ ν − 1 , ν + 3 ≈ ν − 3 α 1 = α 2 = 0.5 \alpha_1=\alpha_2=0.5 α 1 = α 2 = 0.5
k + 1 ( 1 − θ 1 − θ 2 ) e α 1 F E R T = k − 1 θ 1 e ( α 1 − 1 ) F E R T ( A 1 S 2.1 ) k + 3 θ 2 2 = k − 3 ( 1 − θ 1 − θ 2 ) 2 ( A 1 S 2.2 ) \begin{aligned}
k_{+1}(1-\theta_1-\theta_2)e^{\frac{\alpha_1FE}{RT}}&=k_{-1}\theta_1e^{\frac{(\alpha_1-1)FE}{RT}}&(A1S2.1)
\\
k_{+3}\theta_2{}^2&=k_{-3}(1-\theta_1-\theta_2)^2&(A1S2.2)
\end{aligned} k + 1 ( 1 − θ 1 − θ 2 ) e RT α 1 FE k + 3 θ 2 2 = k − 1 θ 1 e RT ( α 1 − 1 ) FE = k − 3 ( 1 − θ 1 − θ 2 ) 2 ( A 1 S 2.1 ) ( A 1 S 2.2 )
可得
V 2 = k + 2 θ 1 e α 2 F E R T = k + 1 k + 2 k + 3 e 3 F E 2 R T k − 1 k + 3 + k − 1 k − 3 + k + 1 k + 3 e F E R T ( A 1 S 2.3 ) \begin{aligned}
V_2&=k_{+2}\theta_1e^{\frac{\alpha_2FE}{RT}}
\\
&=\frac{k_{+1}k_{+2}\sqrt{k_{+3}}e^{\frac{3FE}{2RT}}}{k_{-1}\sqrt{k_{+3}}+k_{-1}\sqrt{k_{-3}}+k_{+1}\sqrt{k_{+3}}e^{\frac{FE}{RT}}}
&(A1S2.3)
\end{aligned} V 2 = k + 2 θ 1 e RT α 2 FE = k − 1 k + 3 + k − 1 k − 3 + k + 1 k + 3 e RT FE k + 1 k + 2 k + 3 e 2 RT 3 FE ( A 1 S 2.3 )
在低过电位区,式 S 2.3 S2.3 S 2.3 e F E R T → 1 e^{\frac{FE}{RT}}\to 1 e RT FE → 1
V = k + 1 k + 2 k + 3 e 3 F E 2 R T k − 1 k + 3 + k − 1 k − 3 + k + 1 k + 3 e F E R T ≈ k + 1 k + 2 k + 3 e 3 F E 2 R T k − 1 k + 3 + k − 1 k − 3 + k + 1 k + 3 = k ′ exp ( 3 F E 2 R T ) ( A 1 S 2.4 ) i F = n F V = 4 F k ′ exp ( 3 F E 2 R T ) ( A 1 S 2.5 ) ∂ Δ E ∂ lg i = 2 × 2.3 R T 3 F = 39 m V ⋅ d e c − 1 \begin{aligned}
V
&=\frac{k_{+1}k_{+2}\sqrt{k_{+3}}e^{\frac{3FE}{2RT}}}{k_{-1}\sqrt{k_{+3}}+k_{-1}\sqrt{k_{-3}}+k_{+1}\sqrt{k_{+3}}e^{\frac{FE}{RT}}}
\\
&\approx
\frac{k_{+1}k_{+2}\sqrt{k_{+3}}e^{\frac{3FE}{2RT}}}{k_{-1}\sqrt{k_{+3}}+k_{-1}\sqrt{k_{-3}}+k_{+1}\sqrt{k_{+3}}}
\\
&=k'\exp\left(\frac{3FE}{2RT}\right)
&(A1S2.4)\\
\\
i_F&=nFV=4Fk'\exp\left(\frac{3FE}{2RT}\right)
&(A1S2.5)\\
\\
\frac{\partial\Delta E}{\partial \lg i }&= \frac{2\times 2.3 RT}{3F}=39 mV\cdot dec^{-1}
\end{aligned} V i F ∂ lg i ∂ Δ E = k − 1 k + 3 + k − 1 k − 3 + k + 1 k + 3 e RT FE k + 1 k + 2 k + 3 e 2 RT 3 FE ≈ k − 1 k + 3 + k − 1 k − 3 + k + 1 k + 3 k + 1 k + 2 k + 3 e 2 RT 3 FE = k ′ exp ( 2 RT 3 FE ) = n F V = 4 F k ′ exp ( 2 RT 3 FE ) = 3 F 2 × 2.3 RT = 39 mV ⋅ d e c − 1 ( A 1 S 2.4 ) ( A 1 S 2.5 )
在高过电位区,式 S 2.4 S2.4 S 2.4 k − 1 k + 3 + k − 1 k − 3 k_{-1}\sqrt{k_{+3}}+k_{-1}\sqrt{k_{-3}} k − 1 k + 3 + k − 1 k − 3
V = k + 1 k + 2 k + 3 e 3 F E 2 R T k − 1 k + 3 + k − 1 k − 3 + k + 1 k + 3 e F E R T ≈ k + 1 k + 2 k + 3 e 3 F E 2 R T k + 1 k + 3 e F E R T = k + 2 exp ( F E 2 R T ) ( A 1 S 2.6 ) i F = n F V = 4 F k + 2 exp ( F E 2 R T ) ( A 1 S 2.7 ) ∂ Δ E ∂ lg i = 2 × 2.3 R T F = 118 m V ⋅ d e c − 1 \begin{aligned}
V
&=\frac{k_{+1}k_{+2}\sqrt{k_{+3}}e^{\frac{3FE}{2RT}}}{k_{-1}\sqrt{k_{+3}}+k_{-1}\sqrt{k_{-3}}+k_{+1}\sqrt{k_{+3}}e^{\frac{FE}{RT}}}
\\
&\approx
\frac{k_{+1}k_{+2}\sqrt{k_{+3}}e^{\frac{3FE}{2RT}}}{k_{+1}\sqrt{k_{+3}}e^{\frac{FE}{RT}}}
\\
&=k_{+2}\exp\left(\frac{FE}{2RT}\right)
&(A1S2.6)\\
\\
i_F&=nFV=4Fk_{+2}\exp\left(\frac{FE}{2RT}\right)
&(A1S2.7)\\
\\
\frac{\partial\Delta E}{\partial \lg i }&= \frac{2\times 2.3 RT}{F}=118 mV\cdot dec^{-1}
\end{aligned} V i F ∂ lg i ∂ Δ E = k − 1 k + 3 + k − 1 k − 3 + k + 1 k + 3 e RT FE k + 1 k + 2 k + 3 e 2 RT 3 FE ≈ k + 1 k + 3 e RT FE k + 1 k + 2 k + 3 e 2 RT 3 FE = k + 2 exp ( 2 RT FE ) = n F V = 4 F k + 2 exp ( 2 RT FE ) = F 2 × 2.3 RT = 118 mV ⋅ d e c − 1 ( A 1 S 2.6 ) ( A 1 S 2.7 )
若 S 3 \mathrm{S3} S3 30 m V ⋅ d e c − 1 30 mV\cdot dec^{-1} 30 mV ⋅ d e c − 1 θ 2 → 1 \theta_2 \to 1 θ 2 → 1 S – O a d s \mathrm{S\text{\textendash}O_{ads}} S – O ads S 3 \mathrm{S3} S3
至此我们完成了对 OER AEM 机理中的复合脱附机理中 Tafel 斜率的推导,由同样方法可推出亲核进攻机理各步骤为决速步时的 Tafel 斜率。我们注意到,复合脱附机理是依据实验中观察到的 Tafel 斜率推断出来的,缺少具有说服力的实验证据;并且因为不同过电位和决速步骤下呈现的 Tafel 斜率可能相同,因此很难仅凭 Tafel 斜率确定反应机理。早在 1983 年,Bockris 等人[2] 就在对钙钛矿型 OER 催化剂的机理研究中提出,复合脱附机理中的最后一步存在问题:
2 S – O a d s = 2 S + O 2 ( A 1 S 3 ) \begin{aligned}
\mathrm{2S\text{\textendash}O_{ads}}&=\mathrm{ 2S + O_2}&(A1S3)
\end{aligned} 2S – O ads = 2S + O 2 ( A 1 S 3 )
并通过理论计算说明,该反应的最大速率远不能达到“快速步”的要求。上文刚刚论述,该步骤为决速步的可能性不大,因此若该步骤不是决速步,则其反应速率应当高于实测的交换电流密度值(约 1 0 − 5 A ⋅ c m − 2 ≈ 1 × 1 0 − 10 m o l ⋅ c m − 2 ⋅ s − 1 10^{-5}A\cdot cm^{-2}\approx 1\times 10^{-10}mol\cdot cm^{-2}\cdot s^{-1} 1 0 − 5 A ⋅ c m − 2 ≈ 1 × 1 0 − 10 m o l ⋅ c m − 2 ⋅ s − 1
v m a x = 2 r O N O 2 v O exp ( − E ∗ / R T ) v_{max}=2r_ON_O{}^2v_O\exp(-E^*/RT)
v ma x = 2 r O N O 2 v O exp ( − E ∗ / RT )
其中, r O r_O r O N O N_O N O v O v_O v O E ∗ E^* E ∗ v O v_O v O v O = 2 k T / π M v_O=\sqrt{2kT/\pi M} v O = 2 k T / π M 1 0 4 c m / s 10^4 cm/s 1 0 4 c m / s N O N_O N O 1 0 14 10^{14} 1 0 14 v m a x ≈ 1 × 1 0 − 18 m o l ⋅ c m − 2 ⋅ s − 1 ≪ 1 × 1 0 − 10 m o l ⋅ c m − 2 ⋅ s − 1 v_{max}\approx 1\times 10^{-18}mol\cdot cm^{-2}\cdot s^{-1}\ll 1\times 10^{-10}mol\cdot cm^{-2}\cdot s^{-1} v ma x ≈ 1 × 1 0 − 18 m o l ⋅ c m − 2 ⋅ s − 1 ≪ 1 × 1 0 − 10 m o l ⋅ c m − 2 ⋅ s − 1
2.1.2 亲核进攻机理(A2)
S + H 2 O = S – O H + H + + e – ( A 2 S 1 ) S – O H = S – O + H + + e – ( A 2 S 2 ) S – O + H 2 O = S – O O H + H + + e – ( A 2 S 3 ) S – O O H = S + O 2 + H + + e – ( A 2 S 4 ) \begin{aligned}
\mathrm{S + H_2O} &= \mathrm{S\text{\textendash}OH + H^+ +e^\text{\textendash}}&(A2S1)
\\
\mathrm{S\text{\textendash}OH} &= \mathrm{S\text{\textendash}O + H^+ + e^\text{\textendash}}&(A2S2)
\\
\mathrm{S\text{\textendash}O+ H_2O} &=\mathrm{ S\text{\textendash}OOH + H^+ + e^\text{\textendash}}&(A2S3)
\\
\mathrm{S\text{\textendash}OOH} &= \mathrm{S + O_2 +H^+ + e^\text{\textendash}}&(A2S4)
\end{aligned} S + H 2 O S – OH S – O + H 2 O S – OOH = S – OH + H + + e – = S – O + H + + e – = S – OOH + H + + e – = S + O 2 + H + + e – ( A 2 S 1 ) ( A 2 S 2 ) ( A 2 S 3 ) ( A 2 S 4 )
如前文所述,酸性条件下亲核进攻机理如上,同理可写出碱性条件下的各反应步骤。不过,无论反应介质是酸性还是碱性,反应均涉及相同的含氧中间体 S – O H \mathrm{S\text{\textendash}OH} S – OH S – O \mathrm{S\text{\textendash}O} S – O S – O O H \mathrm{S\text{\textendash}OOH} S – OOH
Δ G 1 = Δ G S – O H − Δ G H 2 O − e U + k b Tln α H + Δ G 2 = Δ G S – O − Δ G S – O H − e U + k b Tln α H + Δ G 3 = Δ G S – O O H − Δ G S – O − e U + k b Tln α H + Δ G 4 = Δ G O 2 − Δ G S – O O H − e U + k b Tln α H + \begin{aligned}\Delta G_{1}&=\Delta G_{\mathrm{S\text{\textendash}OH}}-\Delta G_{\mathrm{H}_{2} \mathrm{O}}-e \mathrm{U}+k_{\mathrm{b}} \operatorname{Tln} \alpha_{\mathrm{H}^{+}} \\\Delta G_{2}&=\Delta G_{\mathrm{S\text{\textendash}O}}-\Delta G_{\mathrm{S\text{\textendash}OH}}-e \mathrm{U}+k_{\mathrm{b}} \operatorname{Tln} \alpha_{\mathrm{H}^{+}} \\\Delta G_{3}&=\Delta G_{\mathrm{S\text{\textendash}OOH}}-\Delta G_{\mathrm{S\text{\textendash}O}}-e \mathrm{U}+k_{\mathrm{b}} \operatorname{Tln} \alpha_{\mathrm{H}^{+}} \\\Delta G_{4}&=\Delta G_{\mathrm{O}_{2}}-\Delta G_{\mathrm{S\text{\textendash}OOH}}-e \mathrm{U}+k_{\mathrm{b}} \operatorname{Tln} \alpha_{\mathrm{H}^{+}}\end{aligned}
Δ G 1 Δ G 2 Δ G 3 Δ G 4 = Δ G S – OH − Δ G H 2 O − e U + k b Tln α H + = Δ G S – O − Δ G S – OH − e U + k b Tln α H + = Δ G S – OOH − Δ G S – O − e U + k b Tln α H + = Δ G O 2 − Δ G S – OOH − e U + k b Tln α H +
其中吉布斯自由能变最大的步骤为决速步。事实上,我们可以从含氧中间体 S – O H \mathrm{S\text{\textendash}OH} S – OH S – O O H \mathrm{S\text{\textendash}OOH} S – OOH [3] : Δ G S – O O H − Δ G S – O H ≈ 3.2 e V \Delta G_{\mathrm{S\text{\textendash}OOH}}-\Delta G_{\mathrm{S\text{\textendash}OH}}\approx 3.2eV Δ G S – OOH − Δ G S – OH ≈ 3.2 e V S – O H \mathrm{S\text{\textendash}OH} S – OH S – O O H \mathrm{S\text{\textendash}OOH} S – OOH Δ G S – O O H − Δ G S – O H ≈ 3.2 e V \Delta G_{\mathrm{S\text{\textendash}OOH}}-\Delta G_{\mathrm{S\text{\textendash}OH}}\approx 3.2eV Δ G S – OOH − Δ G S – OH ≈ 3.2 e V
Δ G 2 = Δ G S – O − Δ G S – O H − e U + k b Tln α H + Δ G 3 = 3.2 e V − ( Δ G S – O − Δ G S – O H ) − e U + k b Tln α H + \begin{aligned}
\Delta G_{2}&=\Delta G_{\mathrm{S\text{\textendash}O}}-\Delta G_{\mathrm{S\text{\textendash}OH}}-e \mathrm{U}+k_{\mathrm{b}} \operatorname{Tln} \alpha_{\mathrm{H}^{+}} \\\Delta G_{3}&=3.2eV-(\Delta G_{\mathrm{S\text{\textendash}O}}-\Delta G_{\mathrm{S\text{\textendash}OH}})-e \mathrm{U}+k_{\mathrm{b}} \operatorname{Tln} \alpha_{\mathrm{H}^{+}} \end{aligned} Δ G 2 Δ G 3 = Δ G S – O − Δ G S – OH − e U + k b Tln α H + = 3.2 e V − ( Δ G S – O − Δ G S – OH ) − e U + k b Tln α H +
因此可用 Δ G S – O − Δ G S – O H \Delta G_{\mathrm{S\text{\textendash}O}}-\Delta G_{\mathrm{S\text{\textendash}OH}} Δ G S – O − Δ G S – OH Δ G = m a x [ Δ G S – O − Δ G S – O H , 3.2 e V − ( Δ G S – O − Δ G S – O H ) ] \Delta G=max[\Delta G_{\mathrm{S\text{\textendash}O}}-\Delta G_{\mathrm{S\text{\textendash}OH}},\ 3.2eV-(\Delta G_{\mathrm{S\text{\textendash}O}}-\Delta G_{\mathrm{S\text{\textendash}OH}})] Δ G = ma x [ Δ G S – O − Δ G S – OH , 3.2 e V − ( Δ G S – O − Δ G S – OH )] Δ G m i n = 1.6 e V \Delta G_{min}=1.6eV Δ G min = 1.6 e V
η t h e o = 1.6 e V − 1.23 e V e = 0.37 V = 370 m V \eta_{theo}=\frac{1.6eV-1.23eV}{e}=0.37V=370mV
η t h eo = e 1.6 e V − 1.23 e V = 0.37 V = 370 mV
上述推导说明 AEM 机理存在过电势的理论最低值,若希望突破线性约束,则需要开发基于新机理的 OER 催化剂,如下文的 LOM 机理。
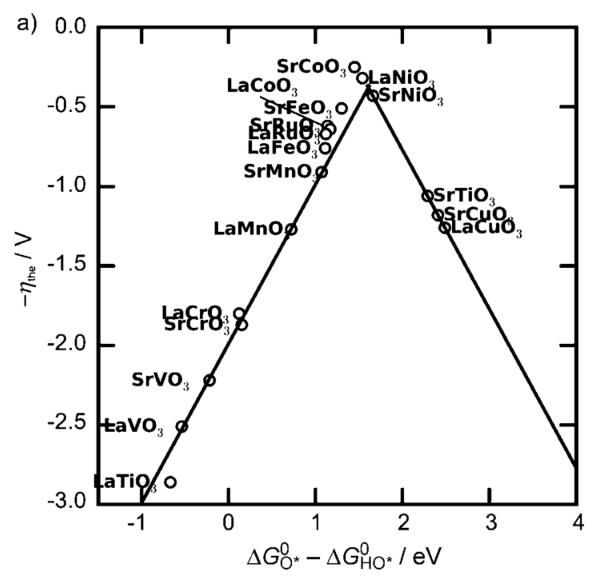
由上述的 Δ G \Delta G Δ G Δ G \Delta G Δ G Δ G S – O − Δ G S – O H \Delta G_{\mathrm{S\text{\textendash}O}}-\Delta G_{\mathrm{S\text{\textendash}OH}} Δ G S – O − Δ G S – OH Δ G S – O − Δ G S – O H \Delta G_{\mathrm{S\text{\textendash}O}}-\Delta G_{\mathrm{S\text{\textendash}OH}} Δ G S – O − Δ G S – OH
图 2 OER 催化剂的火山图,图源[3] 2.2 LOM 机理
2.2.1 LOM 机理概述
LOM(晶格氧机理)与 AEM 机理相比有两点显著不同。一是反应除了质子耦合电子转移过程(PCET)外,还包含非质子耦合电子转移过程(即质子并不随电子的转移而转移,最明显的表现是催化活性与 pH 值相关),二是反应中有催化剂表面晶格氧的参与。在酸性条件下,LOM 机理分为五个步骤:
S + H 2 O = S – O H + H + + e − ( L S 1 ) S – O H = S – O + H + + e − ( L S 2 ) S – O + O L = O 2 + S + V O ( L S 3 ) V O + H 2 O = O L H + H + + e − ( L S 4 ) O L H + e − = O L + H + + e − ( L S 5 ) \begin{aligned}
\mathrm{S + H_2O}&=\mathrm{S\text{\textendash}OH+H^++e^- }&(LS1)
\\
\mathrm{S\text{\textendash}OH }&=\mathrm{S\text{\textendash}O+H^++e^- }&(LS2)
\\
\mathrm{S\text{\textendash}O+O_L }&=\mathrm{O_2+S+V_O }&(LS3)
\\
\mathrm{V_O +H_2O}&=\mathrm{O_LH +H^+ + e^-}&(LS4)
\\
\mathrm{O_LH + e^- }&=\mathrm{O_L + H^+ +e^-}&(LS5)
\end{aligned}
S + H 2 O S – OH S – O + O L V O + H 2 O O L H + e − = S – OH + H + + e − = S – O + H + + e − = O 2 + S + V O = O L H + H + + e − = O L + H + + e − ( L S 1 ) ( L S 2 ) ( L S 3 ) ( L S 4 ) ( L S 5 )
可见,LOM 机理的前两步与 AEM 相同,但第三步中,S – O \mathrm{S\text{\textendash}O} S – O O L O_L O L V O V_O V O 18 O,用其催化 H2 16 O 析氧,则析出的氧气应含有 18 O;邵阳等人[4] 正是使用这种方法,利用在线电化学质谱法(OLEMS)获得了 LOM 机理的实验证据,下面我们就来介绍其详细过程。
2.2.2 LOM 机理的实验证据
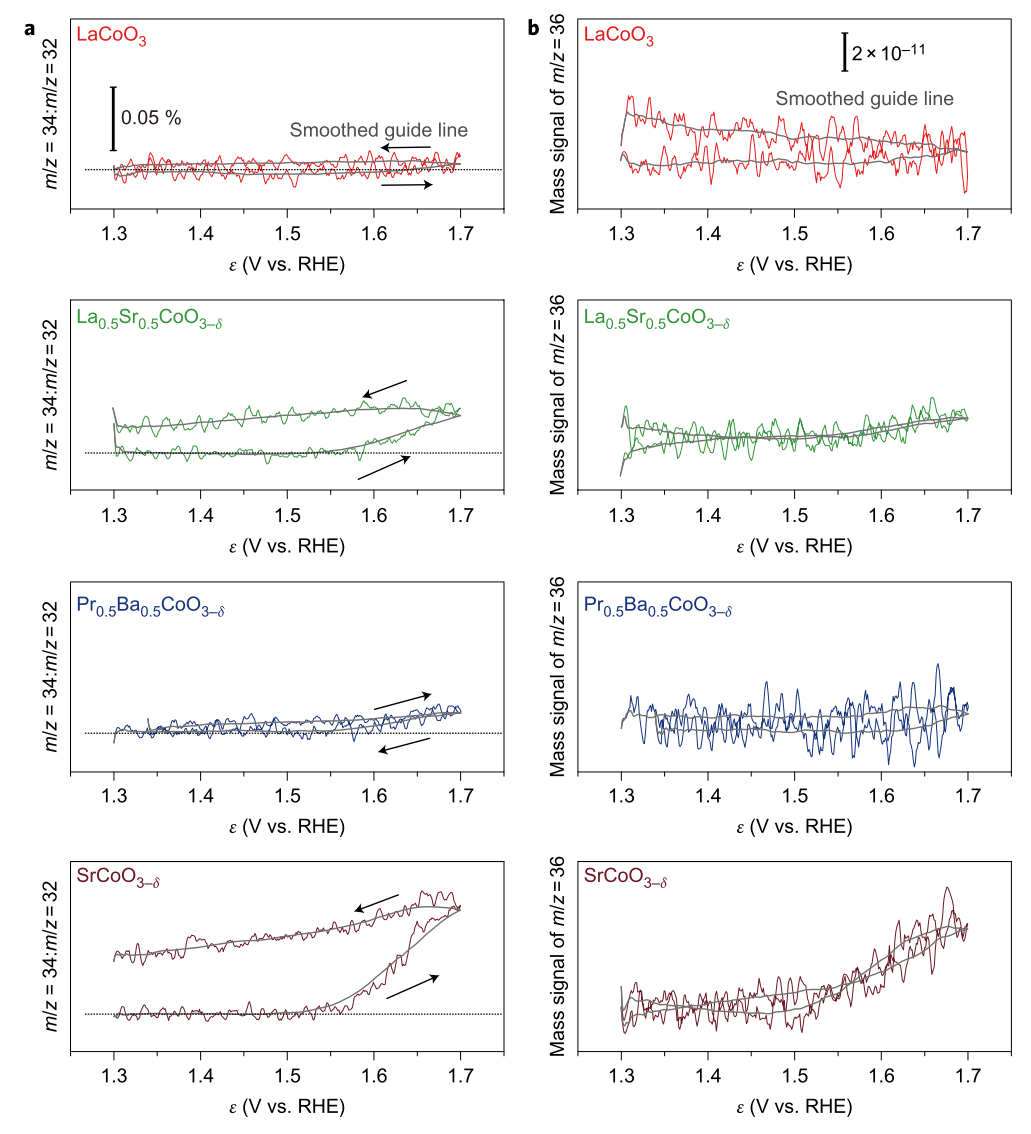
首先,邵阳等人用常规方法合成了 LaCoO3 、、La0.5 Sr0.5 CoO3-δ 、Pr0.5 Ba0.5 CoO3-δ 和SrCoO3-δ 四种钙钛矿型氧化物,并将其负载到金圆盘电极,并在 1.6 V 的电势下将其浸泡在含 H2 18 O的 0.1M KOH 溶液中 10 分钟进行标记,之后用 H2 16 O 洗去电极表面的 H2 18 O,将电极转移至不含 18 O 的 0.1M KOH中进行循环伏安法测试(之后的章节中会介绍)并将阳极产生的气体通入质谱仪。质谱仪中将会出现质荷比为 32,34 和 36 的峰,分别代表 16 O16 O、18 O16 O和18 O18 O。将后两者的信号扣除 18 O 的自然丰度(0.2 %)后与16 O16 O的峰强度作比即可得所产生氧气中实际来自催化剂中的 18 O 的相对含量,只要该值大于 0,就说明产生的氧气中部分氧原子来源于催化剂中的晶格氧,进而证实 LOM 机理。
将不同电势下测得的比值作图可得如下图:
图 3 各种OER催化剂的OLEMS数据,图源[4] 可发现,对于 LaCoO3 ,并没有探测到含 18 O 氧气的生成(曲线未明显远离基线),而其余三种材料按照 Pr0.5 Ba0.5 CoO3-δ 、La0.5 Sr0.5 CoO3-δ 、SrCoO3-δ 的顺序,其产生含 18 O 氧气的比例依次增加,说明它们的 OER 催化机理中 LOM 机理占比不断增加。作者用 DFT 理论计算阐述了催化机理与金属-氧的共价性之间的关系。
2.3 AEM 和 LOM 机理的比较
LOM 机理被认为在提升 OER 活性方面更有前景,因为其包含的 O-O 复合过程可以避开 AEM 机理中活性中间体的能量相关关系,进而有可能突破理论最低过电势的限制。但 LOM 机理由于涉及到催化剂表面的晶格氧,存在着以金属溶出和表面无定形化为代表的等结构不稳定问题,相比而言主要遵循 AEM 机理的 OER 催化剂往往稳定性更高。绝大多数催化剂的催化机理介于 AEM 和 LOM 之间,因此重点在于寻求催化剂活性与稳定性的最佳平衡。
3 参考文献
[1] J. K. Nørskov, T. Bligaard, A. Logadottir, et al. Trends in the Exchange Current for Hydrogen Evolution[J]. Journal of The Electrochemical Society, 2005, 152
[2] J. O. M. Bockris and T. Otagawa. Mechanism of oxygen evolution on perovskites[J]. The Journal of Physical Chemistry, 1983, 87:2960-2971
[3] I. C. Man, H. Y. Su, F. Calle‐Vallejo, et al. Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces[J]. ChemCatChem, 2011, 3:1159-1165
[4] A. Grimaud, O. Diaz-Morales, B. Han, et al. Activating lattice oxygen redox reactions in metal oxides to catalyse oxygen evolution[J]. Nat Chem, 2017, 9:457-465